
We can easily prove this theorem as both the angles formed are right angles.

Let us understand it with the help of the image given below. This theorem states that angles that complement the same angle are congruent angles, whether they are adjacent angles or not. Congruent Complements TheoremĬomplementary angles are those whose sum is 90°. ∴ Angles supplement to the same angle are congruent angles. We can prove this theorem by using the linear pair property of angles, as,įrom the above two equations, we get ∠1 = ∠3. This theorem states that angles supplement to the same angle are congruent angles, whether they are adjacent angles or not. Supplementary angles are those whose sum is 180°. Similarly, we can prove the other three pairs of alternate congruent angles too. When a transversal intersects two parallel lines, each pair of alternate angles are congruent.

It is always stated as true without proof. It's a postulate so we do not need to prove this. When a transversal intersects two parallel lines, corresponding angles are always congruent to each other. The corresponding angles definition tells us that when two parallel lines are intersected by a third one, the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other. (By eliminating ∠1 on both sides)Ĭonclusion: Vertically opposite angles are always congruent angles. If equals are subtracted from equals, the differences are equal. (Transitive: if a=b and b=c that implies a=c) Quantities equal to the same quantity are equal to each other. We already know that angles on a straight line add up to 180°. Proof: The proof is simple and is based on straight angles. Statement: Vertical angles are congruent. Vertical Angles TheoremĪccording to the vertical angles theorem, vertical angles are always congruent. Let's understand each of the theorems in detail along with its proof. Using the congruent angles theorem we can easily find out whether two angles are congruent or not. Theorem 10: If two angles are supplementary to the same angle, or to equal angles, then they are equal to each other.There are many theorems based on congruent angles. Supplementary angles do not need to be adjacent (Figure 8).įigure 8 Nonadjacent supplementary angles.īecause m ∠8 + m ∠9 = 180°, ∠8 and ∠9 are supplementary. Theorem 9: If two adjacent angles have their noncommon sides lying on a line, then they are supplementary angles. Therefore m ∠6 + m ∠7 = 180°, so ∠6 and ∠7 are supplementary. Supplementary angles are two angles whose sum is 180°. Theorem 8 now tells you that m ∠ A = m ∠ C.įigure 5 Two angles complementary to the same angleįigure 6 Two angles complementary to equal angles Also, ∠ C and ∠ D are complementary, and m ∠ B = m ∠ D. In Figure 6, ∠ A and ∠ B are complementary. In Figure 5, ∠ A and ∠ B are complementary. Theorem 8: If two angles are complementary to the same angle, or to equal angles, then they are equal to each other. In Figure 4, because m ∠3 + m ∠4 = 90°, ∠3, and ∠4, are complementary.įigure 4 Nonadjacent complementary anglesĮxample 1: If ∠5 and ∠6 are complementary, and m ∠5 = 15°, find m ∠6. In Figure 3, because ∠ ABC is a right angle, m ∠1 + m ∠2 = 90°, so ∠1 and ∠2 are complementary.Ĭomplementary angles do not need to be adjacent. Theorem 7: Vertical angles are equal in measure.Ĭomplementary angles are any two angles whose sum is 90°. In Figure 2, line l and line m intersect at point Q, forming ∠1, ∠2, ∠3, and ∠4.įigure 2 Two pairs of vertical angles and four pairs of adjacent angles. Any two of these angles that are not adjacent angles are called vertical angles. Vertical angles are formed when two lines intersect and form four angles. In Figure 1, ∠1 and ∠2 are adjacent angles.
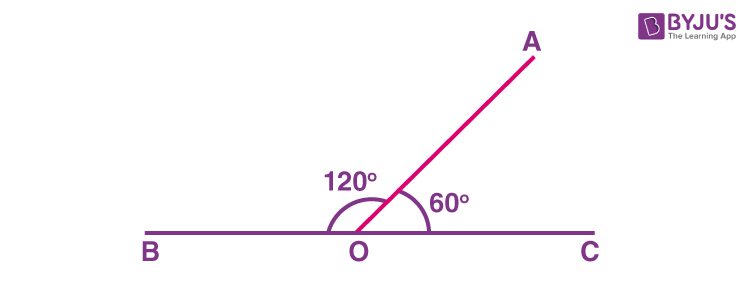
Summary of Coordinate Geometry FormulasĬertain angle pairs are given special names based on their relative position to one another or based on the sum of their respective measures.Īdjacent angles are any two angles that share a common side separating the two angles and that share a common vertex.
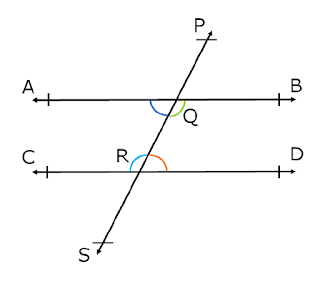
Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Lines: Intersecting, Perpendicular, Parallel.


 0 kommentar(er)
0 kommentar(er)
